Proporção áurea
Proporção áurea: a razão entre a+b e a coincide com a razão entre a e b.
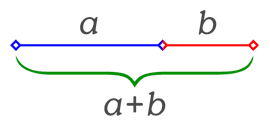
A proporção áurea ou número de ouro ou número áureo ou ainda proporção dourada é uma constante algébrica denotada pela letra grega  (phi) e com o valor arredondado a três casas decimais de 1,618.
(phi) e com o valor arredondado a três casas decimais de 1,618.
 (phi) e com o valor arredondado a três casas decimais de 1,618.
(phi) e com o valor arredondado a três casas decimais de 1,618.
É um número que há muito tempo é empregado na arte. Também é chamada de: razão áurea, razão de ouro, divina proporção, proporção em extrema razão, divisão de extrema razão.
É freqüente a sua utilização em pinturas renascentistas, como as do mestre Giotto. Este número está envolvido com a natureza do crescimento. Phi (não confundir com o número Pi(π), quociente da divisão do comprimento de uma circunferência pela medida do seu respectivo diâmetro), como é chamado o número de ouro, pode ser encontrado na proporção em conchas (o nautilus, por exemplo), seres humanos (o tamanho das falanges,ossos dos dedos, por exemplo), até na relação dos machos e fêmeas de qualquer colméia do mundo, e em inúmeros outros exemplos que envolvem a ordem do crescimento.
Justamente por estar envolvido no crescimento, este número se torna tão freqüente.
E justamente por haver essa freqüência, o número de ouro ganhou um status de “quase mágico”, sendo alvo de pesquisadores, artistas e escritores. Apesar desse status, o número de ouro é apenas o que é devido aos contextos em que está inserido: está envolvido em crescimentos biológicos, por exemplo. O fato de ser encontrado através de desenvolvimento matemático é que o torna fascinante.
Justamente por estar envolvido no crescimento, este número se torna tão freqüente.
E justamente por haver essa freqüência, o número de ouro ganhou um status de “quase mágico”, sendo alvo de pesquisadores, artistas e escritores. Apesar desse status, o número de ouro é apenas o que é devido aos contextos em que está inserido: está envolvido em crescimentos biológicos, por exemplo. O fato de ser encontrado através de desenvolvimento matemático é que o torna fascinante.
Cálculo do Número 

Definição Algébrica
A razão áurea é definida algebricamente como
A equação da direita mostra que  , o que pode ser substituído na parte esquerda, resultando em:
, o que pode ser substituído na parte esquerda, resultando em:
 , o que pode ser substituído na parte esquerda, resultando em:
, o que pode ser substituído na parte esquerda, resultando em:
Cancelando b em ambos os lados, temos:
Multiplicando ambos os lados por  , resulta:
, resulta:
 , resulta:
, resulta:
Finalmente, subtraindo 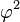 de ambos os membros da equação e multiplicando todas as parcelas por − 1, encontramos:
de ambos os membros da equação e multiplicando todas as parcelas por − 1, encontramos:
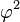 de ambos os membros da equação e multiplicando todas as parcelas por − 1, encontramos:
de ambos os membros da equação e multiplicando todas as parcelas por − 1, encontramos: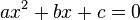 , em que
, em que  .
.
Agora, basta resolver essa equação quadrática. Pela Fórmula de Bháskara
A única solução positiva dessa equação quadrática é a seguinte:
 .
.
Seqüência de Fibonacci
Como é um número extraído da seqüência de Fibonacci, o número áureo representa diretamente uma constante de crescimento.
O número áureo é aproximado pela divisão do enésimo termo da Série de Fibonacci (1,1,2,3,5,8,13,21,34,55,89,…, na qual cada número é a soma dos dois números imediatamente anteriores na própria série) pelo termo anterior. Essa divisão converge para o número áureo conforme tomamos n cada vez maior.
O número áureo é aproximado pela divisão do enésimo termo da Série de Fibonacci (1,1,2,3,5,8,13,21,34,55,89,…, na qual cada número é a soma dos dois números imediatamente anteriores na própria série) pelo termo anterior. Essa divisão converge para o número áureo conforme tomamos n cada vez maior.
Origem do nome
Phi tem este nome em homenagem ao arquiteto grego Phidias, construtor do Parthenon, que utilizou o número de ouro em muitas de suas obras.
Proporção Áurea na Natureza
Por que esse número é tão apreciado por artistas, arquitetos, projetistas e músicos? Porque a proporção áurea, como o nome sugere, está presente na natureza, no corpo humano e no universo.
Este número, assim como outros, por exemplo o Pi, estão presentes no mundo por uma razão matemática existente na natureza.
Essa seqüência aparece na natureza, no DNA, no comportamento da refração da luz, dos átomos, nas vibrações sonoras, no crescimento das plantas, nas espirais das galáxias, dos marfins de elefantes, nas ondas no oceano, furacões, etc.
Por que esse número é tão apreciado por artistas, arquitetos, projetistas e músicos? Porque a proporção áurea, como o nome sugere, está presente na natureza, no corpo humano e no universo.
Este número, assim como outros, por exemplo o Pi, estão presentes no mundo por uma razão matemática existente na natureza.
Essa seqüência aparece na natureza, no DNA, no comportamento da refração da luz, dos átomos, nas vibrações sonoras, no crescimento das plantas, nas espirais das galáxias, dos marfins de elefantes, nas ondas no oceano, furacões, etc.
Figuras Geométricas
Um decágono regular, inscrito numa circunferência, tem os lados em relação dourada com o raio da circunferência.
Um decágono regular, inscrito numa circunferência, tem os lados em relação dourada com o raio da circunferência.

Um pentagrama regular é obtido traçando-se as diagonais de um pentágono regular. O pentágono menor, formado pelas interseções das diagonais, também está em proporção com o pentágono maior, de onde se originou o pentagrama. A razão entre as medidas dos lados dos dois pentágonos é igual ao quadrado da razão áurea. A razão entre as medidas das áreas dos dois pentágonos é igual a quarta potência da razão áurea.
Chamando os vértices de um pentagrama de A, B, C, D e E, o triângulo isósceles formado por A, C e D tem seus lados em relação dourada com a base, e o triângulo isósceles A, B e C tem sua base em relação dourada com os lados.
Quando Pitágoras descobriu que as proporções no pentagrama eram a proporção áurea, tornou esse símbolo estrelado como a representação da Irmandade Pitagórica. Esse era um dos motivos que levava Pitágoras a dizer que “tudo é número”, ou seja, que a natureza segue padrões matemáticos.
A maçonaria também tomou emprestado o simbolismo da Proporção Dourada em seus ensinamentos, com a utilização de seu método para obtenção do Pentagrama e do Quadrado Oblongo, existentes em algumas Lojas Maçônicas.
Vegetais
Semente de girassol – A proporção em que aumenta o diâmetro das espirais de sementes de um girassol é a razão áurea.
Achillea ptarmica – Razão do crescimento de seus galhos.
Folhas das Árvores – A proporção em que diminuem as folhas de uma árvore à medida que subimos de altura.
Semente de girassol – A proporção em que aumenta o diâmetro das espirais de sementes de um girassol é a razão áurea.
Achillea ptarmica – Razão do crescimento de seus galhos.
Folhas das Árvores – A proporção em que diminuem as folhas de uma árvore à medida que subimos de altura.
Animais
População de Abelhas – A proporção entre abelhas fêmeas e machos em qualquer colméia.
Concha do Caramujo Nautilus – A proporção em que cresce o raio do interior da concha desta espécie de caramujo. Este moluscobombeia gás para dentro de sua concha repleta de câmaras para poder regular a profundidade de sua flutuação.
Outros – phi estão também nas escamas de peixes, presas de elefantes, crescimento de plantas.
População de Abelhas – A proporção entre abelhas fêmeas e machos em qualquer colméia.
Concha do Caramujo Nautilus – A proporção em que cresce o raio do interior da concha desta espécie de caramujo. Este moluscobombeia gás para dentro de sua concha repleta de câmaras para poder regular a profundidade de sua flutuação.
Outros – phi estão também nas escamas de peixes, presas de elefantes, crescimento de plantas.
Corpo Humano
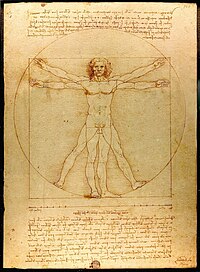

O Homem Vitruviano, de Leonardo da Vinci. As idéias de proporção e simetria aplicadas à concepção da beleza humana
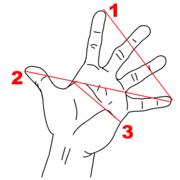
Proporções áureas em uma mão
A altura do corpo humano e a medida do umbigo até o chão.
A altura do crânio e a medida da mandíbula até o alto da cabeça.
A medida da cintura até a cabeça e o tamanho do tórax.
A medida do ombro à ponta do dedo e a medida do cotovelo à ponta do dedo.
O tamanho dos dedos e a medida da dobra central até a ponta.
A medida da dobra central até a ponta dividido e da segunda dobra até a ponta.
A medida do seu quadril ao chão e a medida do seu joelho até ao chão.
A medida do cotovelo até o pulso e a medida do seu pé
Essas proporções anatômicas foram bem representadas pelo “Homem Vitruviano”, obra de Leonardo Da Vinci.
A medida da cintura até a cabeça e o tamanho do tórax.
A medida do ombro à ponta do dedo e a medida do cotovelo à ponta do dedo.
O tamanho dos dedos e a medida da dobra central até a ponta.
A medida da dobra central até a ponta dividido e da segunda dobra até a ponta.
A medida do seu quadril ao chão e a medida do seu joelho até ao chão.
A medida do cotovelo até o pulso e a medida do seu pé
Essas proporções anatômicas foram bem representadas pelo “Homem Vitruviano”, obra de Leonardo Da Vinci.
Aplicações
O homem sempre tentou alcançar a perfeição, seja nas pinturas, seja nos projetos arquitetônicos, seja até mesmo na música.
O homem sempre tentou alcançar a perfeição, seja nas pinturas, seja nos projetos arquitetônicos, seja até mesmo na música.
Arte
A proporção áurea foi muito usada na arte, em obras como O Nascimento de Vênus, quadro de Botticelli, em que Afrodite está na proporção áurea. Essa proporção estaria ali aplicada pelo motivo de o autor representar a perfeição da beleza. Em O Sacramento da Última Ceia, de Salvador Dalí, as dimensões do quadro (aproximadamente 270 cm × 167 cm) estão numa Razão Áurea entre si. Na história da arterenascentista, a perfeição da beleza em quadros foi bastante explorada com base nessa constante. Vários pintores e escultores lançaram mão das possibilidades que a proporção lhes dava para retratar a realidade com mais perfeição.
A proporção áurea foi muito usada na arte, em obras como O Nascimento de Vênus, quadro de Botticelli, em que Afrodite está na proporção áurea. Essa proporção estaria ali aplicada pelo motivo de o autor representar a perfeição da beleza. Em O Sacramento da Última Ceia, de Salvador Dalí, as dimensões do quadro (aproximadamente 270 cm × 167 cm) estão numa Razão Áurea entre si. Na história da arterenascentista, a perfeição da beleza em quadros foi bastante explorada com base nessa constante. Vários pintores e escultores lançaram mão das possibilidades que a proporção lhes dava para retratar a realidade com mais perfeição.
A Mona Lisa, de Leonardo da Vinci, utiliza o número áureo nas relações entre seu tronco e cabeça, e também entre os elementos do rosto.
Literatura
Na literatura, o número de ouro encontra sua aplicação mais notável no poema épico grego Ilíada, de Homero, que narra os acontecimentos dos últimos dias da Guerra de Tróia. Quem o ler notará que a proporção entre as estrofes maiores e as menores dá um número próximo a 1,618, o número de ouro.
Luís de Camões na sua obra Os Lusíadas, colocou a chegada à Índia no ponto que divide a obra na razão de ouro.
Virgílio em sua obra Eneida, construiu a razão áurea com as estrofes maiores e menores.
Na literatura, o número de ouro encontra sua aplicação mais notável no poema épico grego Ilíada, de Homero, que narra os acontecimentos dos últimos dias da Guerra de Tróia. Quem o ler notará que a proporção entre as estrofes maiores e as menores dá um número próximo a 1,618, o número de ouro.
Luís de Camões na sua obra Os Lusíadas, colocou a chegada à Índia no ponto que divide a obra na razão de ouro.
Virgílio em sua obra Eneida, construiu a razão áurea com as estrofes maiores e menores.
Retângulo Dourado
Proporção áurea em retângulos
Trata-se do retângulo no qual a proporção entre o comprimento e a largura é aproximadamente o número Phi, ou seja, 1,618, que reflete também as proporções do Parténon.

Os Egípcios fizeram o mesmo com as pirâmides. Por exemplo, cada bloco da pirâmide era 1,618 vezes maior que o bloco do nível logo acima. As câmaras no interior das pirâmides também seguiam essa proporção, de forma que os comprimentos das salas são 1,618 vezes maiores que as larguras.
Música
O número de ouro está presente nas famosas sinfonias Sinfonia n.º 5 e a Sinfonia n.º 9, de Ludwig van Beethoven, e em outras diversas obras. Outro fato interessante registrado na Revista Batera, em um artigo sobre o baterista de jazz Max Roach, é que, em seus solos curtos, aparece tal número, se considerarmos as relações que aparecem entre tempos de bumbo e caixa.
O número de ouro está presente nas famosas sinfonias Sinfonia n.º 5 e a Sinfonia n.º 9, de Ludwig van Beethoven, e em outras diversas obras. Outro fato interessante registrado na Revista Batera, em um artigo sobre o baterista de jazz Max Roach, é que, em seus solos curtos, aparece tal número, se considerarmos as relações que aparecem entre tempos de bumbo e caixa.
Cinema
O diretor russo Sergei Eisenstein se utilizou do número no filme O Encouraçado Potemkin para marcar os inícios de cenas importantes da trama, medindo a razão pelo tamanho das fitas de película.
no filme O Encouraçado Potemkin para marcar os inícios de cenas importantes da trama, medindo a razão pelo tamanho das fitas de película.
O diretor russo Sergei Eisenstein se utilizou do número
 no filme O Encouraçado Potemkin para marcar os inícios de cenas importantes da trama, medindo a razão pelo tamanho das fitas de película.
no filme O Encouraçado Potemkin para marcar os inícios de cenas importantes da trama, medindo a razão pelo tamanho das fitas de película.
Objetos Atuais
Atualmente, essa proporção ainda é muito usada. Ao padronizar internacionalmente algumas medidas usadas em nosso dia-a-dia, os projetistas procuraram “respeitar” a proporção divina. A razão entre o comprimento e a largura de um Cartão de Crédito, alguns livros, jornais, uma foto revelada, entre outros.
Atualmente, essa proporção ainda é muito usada. Ao padronizar internacionalmente algumas medidas usadas em nosso dia-a-dia, os projetistas procuraram “respeitar” a proporção divina. A razão entre o comprimento e a largura de um Cartão de Crédito, alguns livros, jornais, uma foto revelada, entre outros.
Efeitos
Algumas das correntes místicas acreditam que objetos cujas dimensões sejam relacionadas a Phi se harmonizam com a glândula pineal, o que provocaria ou estimularia uma sensação de beleza e harmonia no ser humano.
Algumas das correntes místicas acreditam que objetos cujas dimensões sejam relacionadas a Phi se harmonizam com a glândula pineal, o que provocaria ou estimularia uma sensação de beleza e harmonia no ser humano.
Oi prof. claro que sim. Será uma honra, vou ficar orgulhosa de ver meu nome e meu trabalho no seu blog que para mim é uma fonte cultural.Eu tenho aprendido muito com seus posts.Fico muito feliz e te desejo boa sorte.bjs Tenha um lindo domingo e uma ótima semana
ResponderExcluiroi prof.Selione. Gostaria da sua opinião sincera sobre a última postagem que fiz - INOCÊNCIA - Assim posso me aperfeiçoar e continuar tentando escrever.bjs.
ResponderExcluirOi prof.Selione, gostaria muito de ter sua opinião sobre o meu último texto publicado. INOCÊNCIA - Assim continuarei tentando escrever já que é o que mais gosto de fazer.obrigada
ResponderExcluir